Union (mengdelære)
I denne artikkelen vil vi utforske temaet Union (mengdelære) i dybden, og ta for seg dets opprinnelse, utvikling og relevans i dag. Siden fremveksten har Union (mengdelære) fanget interessen til akademikere, spesialister og allmennheten, og utløst debatter, refleksjoner og fremskritt på ulike felt. Union (mengdelære) har gjennom årene vist seg å være et tema av stor betydning, både for påvirkning på samfunnet og påvirkning på ulike kunnskapsområder. Gjennom denne omfattende analysen vil vi søke å forstå betydningen av Union (mengdelære) og dens rolle i en verden i stadig endring.
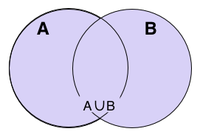
Innenfor matematikken er unionen (eller foreningsmengden) mellom to mengder A og B, mengden av alle elementer som ligger i A, B eller både A og B.
Unionen mellom A og B skrives A ∪ B. For alle A gjelder at A ∪ Ø = A og at A ∪ A = A.
Eksempler
- {A, B, C, D} ∪ {C, D, E} = {A, B, C, D, E}
- {x | x er et partall} ∪ {x | x er et oddetall} = {x | x er et heltall}
- {x | x er et menneske} ∪ {x | x er norsk statsborger} = {x | x er et menneske} (alle elementene i den andre mengden er inneholdt i den første).
Se også
- Snitt
- Mengdelære
- Mengdedifferanse, mengden man får dersom man fjerner elementene i en bestemt mengde fra en annen mengde