Hendelse

I denne artikkelen skal vi fordype oss i temaet Hendelse, som har vakt stor interesse på ulike områder. Hendelse er et tema som har fanget oppmerksomheten til akademikere, fagfolk og allmennheten på grunn av dets relevans og gjennomslagskraft i dagens samfunn. Hendelse har gjennom årene skapt debatt og refleksjon i ulike sammenhenger, fra historiske problemstillinger til teknologiske aspekter. I denne artikkelen vil vi analysere ulike perspektiver og tilnærminger til Hendelse, med sikte på å forstå dens betydning og implikasjoner i dag.

B er utfallsrommet og A er en hendelse. Hvis sannsynligheten er proporsjonal med arealet, er sannsynligheten for A omtrent 0,4.

Hendelse (fra hende (+ -else), norrønt henda, avledet av hǫnd (hånd); grunnbetydning «berøre med hånden»)[1] henviser til noe som hender; begivenhet eller tildragelse.[1] Hendelse er alt som skjer, spesielt noe viktig eller uvanlig: sportshendelse som cupfinalen i fotball; sosial hendelse som et bryllup, eller en rekke av hendelser, som politiets undersøkelser av særskilt kriminalitet.[2][3]

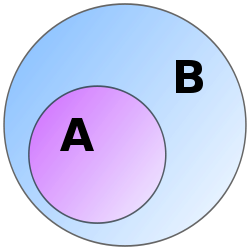
I sannsynlighetsteori betegner en hendelse et sett med utfall av et eksperiment (en delmengde av utfallsrommet) som en sannsynlighet er tildelt.[4] Et enkelt utfall kan være et element av mange forskjellige hendelser,[5] og forskjellige hendelser i et eksperiment er vanligvis ikke like sannsynlige, siden de kan omfatte svært forskjellige grupper av utfall.[6]

For et terningkast er for eksempel utfallsrommet mengden {1, 2, 3, 4, 5, 6}. En hendelse kan være at man kaster et partall. Denne hendelsen er da mengden {2, 4, 6}. En hendelse som kun består av ett enkelt utfall kalles en elementær hendelse; det vil si at det er et enkeltsett. En hendelse som har mer enn ett mulig utfall kalles en sammensatt hendelse.

Hendelser i sannsynlighetsrom

I elementær sannsynlighetsteori holder det med den intuitive definisjonen ovenfor, men ofte er det behov for en mer presis forståelse av hendelser.

Hvis Ω er utfallsrommet til et tilfeldig eksperiment, definerer man de mulige hendelsene som elementene i en σ-algebra F. Hvis utfallsrommet er endelig, som i eksempelet med terningen ovenfor, kan man la F være potensmengden til Ω, det vil si mengden av alle undermengder av Ω. Men hvis Ω er uendelig er potensmengden for stor, så F inneholder ikke alle mulige undermengder av Ω.

Referanser

  1. ^ a b «hendelse», «hende», NAOB
  2. ^ «event», Dictionary Cambridge
  3. ^ «event», Oxford English Dictionary
  4. ^ Leon-Garcia, Alberto (2008): Probability, statistics and random processes for electrical engineering. Upper Saddle River, NJ: Pearson. ISBN 9780131471221.
  5. ^ Pfeiffer, Paul E. (1978): Concepts of probability theory. Dover Publications. ISBN 978-0-486-63677-1; s. 18.
  6. ^ Foerster, Paul A. (2006): Algebra and trigonometry: Functions and Applications, Teacher's edition (Classics ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-165711-9; s. 634.

Eksterne lenker